PEMBAHASAN:
- Sifat Alamiah
- Perfect & Imperfect
- Konsekuensi 
- Deteksi Multikolinieritas
- Alternatif Solusi

A. SIFAT ALAMIAH
        Misalkan regresi pengeluaran untuk konsumsi makanan keluarga pada pendapatan keluarga, tabungan, usia kepala keluarga. Variabel independen akan saling berkorelasi. Variabel independen juga berkorelasi dengan variabel sosial-ekonomi lain yang berpengaruh terhadap pengeluaran untuk konsumsi, misalkan ukuran keluarga → Terjadi Multikolinieritas (kolinieritas). Salah satu asumsi OLS adalah berkaitan dengan tidak adanya Multikolinieritas.

B. MULTIKOLINIERTITAS SEMPURNA
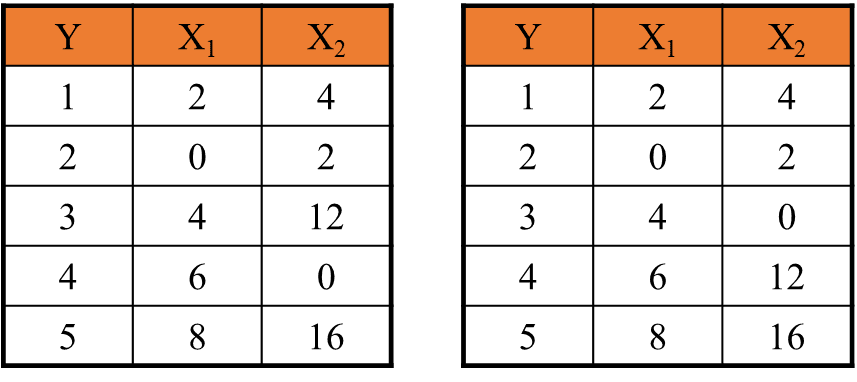
Ditemukan pertama kali oleh Ragnar Frisch (Institute of Economics, Oslo University). Pada awalnya, multikolinieritas berarti adanya hubungan yg linier sempurna atau pasti diantara beberapa atau semua variabel bebas dalam model regresi. Misalkan pada model regresi dengan k variabel bebas X1, X2, …, Xk (dimana X1 = 1), suatu hubungan linier yg sempurna dikatakan ada jika memenuhi kondisi:
Koefisien regresi tidak dapat diestimasi dan standart errornya tidak berhinggga. Misal pada pertemuan sebelumnya :
Begitu pula dengan 𝜷𝟐 tidak dapat diestimasi. Ilustrasi multikolinieritas sempurna dengan mengasumsikan :
𝜷 ̂𝟏 laju perubahan rata-rata nilai Y seiring dengan berubahnya nilai 𝑿𝟏 dengan 𝑿𝟐 dianggap konstant.
Padahal 𝑿𝟐 akan berubah seiring dengan 𝑿𝟏 yang berubah pula dengan faktor λ. 
        Pandangan Ballentine dalam ringkasan sebuah gambar:

C. MULTIKOLINIERTITAS TIDAK  SEMPURNA
        Perkembangannya, multikolinieritas juga berarti adanya hubungan yg linier kuat tetapi tidak sempurna diantara beberapa atau semua variabel bebas dalam model regresi. Misalkan pada model regresi dengan k variabel bebas X1, X2, …, Xk. (dimana X1 = 1), suatu hubungan linier yg kuat tapi tidak sempurna dikatakan ada jika memenuhi kondisi:
dimana vi adalah unsur kesalahan yg bersifat stokastik.
Misalkan kita ambil contoh persamaan berikut:
1. Estimasi koefisien regresi masih dapat dilakukan dengan :
  
     Begitu pula dengan 𝜷 ̂𝟐.  Namun demikian tetap berkonsekuensi varian dan kovarian yang besar. 
2. Varian dan kovarian yang besar dari estimator.
Misal 𝒓𝟏𝟐 = 0, 𝒓𝟏𝟐 = 0,5 , 𝒓𝟏𝟐 = 0,9, dan 𝒓𝟏𝟐 = 1, tbegitupun  varian, se, dan covariannya. 
3. Besarnya standard error berakibat, interval estimasi cenderung menjadi lebih lebar. 
4. Uji t cenderung tidak signifikan. 
 semakin kecil dan kemungkinan lebih kecil dari pada t- tabel.
5.Estimator  & standard error menjadi sensitif terhadap perubahan data
        Multikolinieritas yg tinggi tapi tidak sempurna,  estimator koefisien regresi bisa diperoleh, tapi estimator  & standard error menjadi sensitif terhadap perubahan data.
Misalkan:
Estimasi tabel diatas, kemudian bandingkan signifikansi koefisien regresi, s.e., & R2 maka terjadi perubahan yang ekstrem.
6. 𝑹𝟐 (koefisien determinasi) tinggi namun tidak  satupun variabel signifikan secara statistik
         Pada multikolinieritas yg tinggi tapi tidak sempurna, bisa  terjadi 𝑹𝟐 (koefisien determinasi) tinggi namun tidak  satupun variabel signifikan secara statistik. Uji t tidak siginifikan tapi uji F secara meyakinkan signifikan.  Perlu diingat hubungan 𝑭 dan 𝑹^𝟐 kaitannya dengan uji F.

D. PENDETEKSIAN  MULTIKOLINIERITAS
1.   Nilai 𝑹𝟐 tinggi sebagian Var. Independen Tidak Signifikan
Contoh 1: 
Kemudian setelah kita estimasi dengan program eview, didapatkan ringkasan hasil regresi sebagai berikut: 
Berdasarkan hasil regresi tersebut, pendapatan positif (sesuai teori), kekayaan negatif (tidak sesuai teori), Uji t masing-masing variabel independen tidak signifikan, meskipun Uji F signifikan. Maka dapat dikatakan bahwa model regresi mengandung masalah multikolinieritas.
2.   Korelasi Parsial antar Variabel Independen
Contoh 2: 
Hasil regresi: 
Berdasarkan hasil regresi tersebut, semua tanda keofisien sesuai teori, uji t masing-masing variabel independen signifikan, begitupun Uji F signifikan. Maka dapat disimpulkan bahwa model regresi tidak terdapat masalah multikolinieritas.

3. Regresi Auxiliary
        Digunakan untuk mengetahui apakah variabel independen X yang satu berhubungan dengan variabel X yang lain dengan cara melakukan regresi setiap variabel independen X dengan sisa variabel independen X yang lain.        
Langkah-langkah:
        1. Estimasi setiap var X dengan sisa var X yang lain 
        2. Pergunakan masing-masing nilai 𝑹𝟐 untuk mengitung F hitung
        3. Kemudian bandingkan F hitung dengan F tabel dengan 𝛼 dan df tertentu
        4. Kesimpulan :
                 F hitung >  F tabel (mengandung unsur multikolinieritas
                 F hitung <  F tabel (tidak mengandung unsur multikolinieritas)
Contoh: 

4. Metode Klien
        Multikolinieritas terjadi jika nilai koefisien determinasi (𝑹𝟐) pada  regresi Auxiliary > nilai koefisien determinasi (𝑹𝟐) regresi biasa. Dan sebaliknya jika <  maka tidak terdapat multikolinieritas.
Pada contoh 3, nilai koefisien determinasi 𝑹𝟐 Auxiliary untuk masing masing X  adalah 
Sedangkan untuk nilai koefisien determinasi 𝑹𝟐  regresi biasa = 0,6610 (didapatkan dari contoh 2) Karena semua  𝑹𝟐Auxiliary < 𝑹𝟐  regresi biasa, berarti dapat disimpulkan tidak terdapat multikolinieritas.

5. VIF dan TOL
        Jika nilai VIF semakin besar (>10)  maka diduga terdapat multikolinieritas. Dan sebaliknya jika kecil (<10) maka diduga tidak terdapat multikolinieritas.
Keterangan: 𝑹𝟐𝑗 = 𝑹𝟐 pada regresi Auxiliary
Sedangkan untuk nilai TOL jika menzdekati 1 maka diduga tidak terdapat multikolinieritas, dan jika mendekati 0 maka diduga terdapat multikolinieritas.
Berdasarkan 𝑹𝟐 pada regresi Auxiliary (contoh 3), maka VIF dapat dicari dengan cara berikut:

E. Solusi  Multikolinieritas

1. Informasi Apriori
Misalkan : 

 Keterangan;
Y  =  Konsumsi,
X1 = Pendapatan
X2 = Tabungan
Informasi apriori, misalkan β2 = 0,10β1  sehingga Yi = β0+ β1 Xi1+ 0,10 β2 X2i + ei = β0 + β1 Xi +ei
dimana Xi = X1i + 0,10 X2i.  Saat kita mendapatkan nilai β1 maka kita dapat mengestimasi β2 berdasarkan informasi apriori.  Informasi apriori  bisa berdasarkan studi empiris suatu teori atau hasil penelitian sebelumnya
2. Kombinasi Data 
Menghubungkan data cross-sectional dan data time series (panel data).
3. Menghilangkan variabel
            Mengeluarkan satu atau beberapa variabel independen. Namun dampaknya bisa lebih buruk dari pada masalah multikolinieritas itu sendiri, karena terjadi bias spesifikasi. Beberapa metode yg dapat digunakan:  Principle Component Analysis, Factor Analysis,Stepwise Regression, Ridge Regression  dan lain sebagainya.
4. Transformasi variabel
    Transformasi variabel (melalui first differencing);
    Transformasi rasio;
5. Penambahan Data
Dengan meningkatkan ukuran sampel jika varian dirumuskan sebagai: 
Maka  juga akan menigkat, sehingga memperkecil varian  dan standart error. Sehingga estimasinya akan lebih tepat. Sebagai contoh: 
Hasil awal mengandung multikolinieritas:
Namun setelah ditambahkan suatu data sejumlah 40, maka hasil tidak lagi mengandung masalah multikolinieritas.

VIDEO PEMBELAJARAN PEMBAHASAN MATERI DI ATAS


DAFTAR PUSTAKA.
  • Gunawan Sumodiningrat, 2003, Ekonometrika, BPFE, Yogyakarta.
  • Gujarati, D.N., 2007, Dasar-Dasar Ekonometrika, Edisi Ketiga, Jilid-1 dan Jilid-2, Terjemahan Julius A. Mulyadi; Penerbit Erlangga.Jakarta.
  • Agus Widarjono, 2009, Ekonometrika : Pengantar dan Aplikasinya, Penerbit Ekonisia, Fakultas Ekonomi, UII, Yogyakarta.
  • Nachrowi Djalal Nachrowi dan Hardius Usman, 2002,  Penggunaan Teknik Ekonometri.  LPFE -UI. Jakarta.