A. FUNGSI NON LINIER
Fungsi Non Linier adalah hubungan matematis antara satu variabel dengan variabel lainnya yang grafik kurvanya tidak berbentuk garis lurus.Bentuk persamaan fungsi non linier terdiri dari variabel/ bilangan berpangkat lebih dari 1. Bentuk persamaan fungsi non linier terdiri dari variabel/ bilangan berpangkat lebih dari 1 disebut juga sebagai polinom atau suku banyak. Menggambarkan kurva non linier tidak semudah kurva fungsi linier. Bentuk kurva dalam fungsi non linier bukan garis melainkan garis lengkung. Bentuk bentuk fungsi Non Linier yang paling sering dijumpai dalam analaisis ekonomi adalah :
1. Fungsi Kuadrat/Parabolik
2. Fungsi Kubik
3. Fungsi Eksponensial
4. Logaritma
1). Tabel Titik Titik Yang Banyak (Curve Traicing Proccess)
Misalkan akan menggambarkan grafik kurva dari fungsi :
- Menggambarkan masing-masing titik dalam koordinat cartesius
- Menghubungkan titik-titik tersebut dengan kurva melengkung.
- Hasil kurva seperti gambar di bawah.
- Namun cara ini masih banyak kekurangan terutama pada fungsi dengan x berpangkat lebih 2, misalnya fungsi kubik, quadratic, dan lain-lain.
- Terlebih kita tidak tahu titik puncak kurva tersebut.
2). Kaidah-kaidah Matematis
Terdapat beberapa kaidah matematis dalam menggambarkan kurva non-linier:
a. Titik Penggal/Titik Potong dengan Sumbu X dan atau Y
- Titik potong dengan sumbu x dapat dicari dengan memisalkan y = 0
- Titik potong dengan sumbu y dapat dicari dengan memisalkan x = 0
Contoh 1: Misalkan akan menggambarkan grafik kurva dari fungsi:
Untuk mencari titik potong terhadap sumbu X dan atau Y dari fungsi non-linier tersebut adalah sebagai berikut:
b. Titik dan Kurva Simetris
Dua titik dikatakan simetris terhadap suatu garis bila garis tersebut terletak di antara dua titik dan jaraknya sama. Titik O (0,0) disebut sebagai titik Origin. Suatu kurva dikatakan simteris jika setiap titik kurva tersebut tercermin pada garis tertentu . Berikut ilustrasi titik atau kurva yang simetris.
c. Batas Nilai
Suatu fungsi dapat mempunyai nilai riil atau imajiner. Pada masalah nilai imajiner nilainya tidak dapat ditentukan sehingga terdapat batas nilai.
Contoh 2:
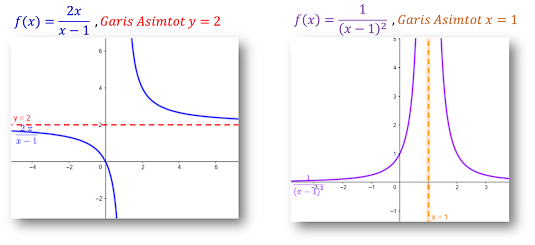
d. Asimtot
Asimtot suatu kurva adalah sebuah garis yang sedemikian rupa sehingga jarak antara kurva dan garis tersebut mendekati nol seiring x atau y (salah satu atau keduanya) mendekati tak berhingga. Garis asimtot yang digunakan umumnya merupakan garis yang sejajar dengan sumbu x dan sumbu y.
Contoh 3:
e. Faktorisasi
Persamaan kurva f(x,y)=0 dapat terdiri dari hasil perkalian antar dua faktor atau lebih. Maka grafik fungsi tersebut dapat terdiri dari dua grafik g(x,y)=0 dan h(x,y)=0 dan titik (x,y) yang memenuhi persamaan grafik g(x,y)=0 dan h(x,y)=0 .
Contoh 4:
Buatlah grafik dengan menjabarkan 3𝑥𝑦 menjadi −xy+4𝑥𝑦 dari fungsi berikut:
B. FUNGSI KUADRAT
Suatu persamaan kuadrat dapat berupa lingkaran, elips, parabola, hiperbola, atau bentuk lainnya. Bentuk umum persamaan kuadratik:
dengan 𝐴,𝐵,𝐶,𝐷, 𝐸, 𝑑𝑎𝑛 𝐹 adalah konstanta dan paling tidak salah satu dari 𝐴,𝐵,𝐶≠0.
Dari persamaan umum kuadratik, jika :
1. B = 0 dan A= C , maka persamaan berbentuk Lingkaran
2. 𝐵^2−4𝐴𝐶 < 0 , maka irisan berbentuk elips.
3. 𝐵^2−4𝐴𝐶 = 0 , maka irisan berbentuk parabola.
4. 𝐵^2−4𝐴𝐶 > 0 , maka irisan berbentuk hiperbola.
atau
(h,k) pusat lingkaran.
Contoh 5 :
Tentukan titik pusat dan jari-jari dari lingkaran berikut:
2. Elips
Elips adalah tempat kedudukan titik-titik pada bidang datar yang jumlah jaraknya dari dua buah titik tertentu tetap. Titik tertentu disebut Titik Fokus. Bentuk umum persamaan elips:
atauAtau bentuk standar :
Contoh 7: Tentukan titik pusat dan pers. asimtotnya hiperbola:
Atau bentuk standar :
Contoh 6:
Tentukan titik pusat dan jari-jari Panjang dan lebar elips :
3. Hiperbola
Hiperbola adalah tempat kedudukan titik-titik pada bidang datar yang selisih jaraknya terhadap dua buah titik tertentu besarnya tetap. Titik tertentu disebut Titik Fokus. Bentuk umum persamaan hiperbola:
Contoh 7: Tentukan titik pusat dan pers. asimtotnya hiperbola:
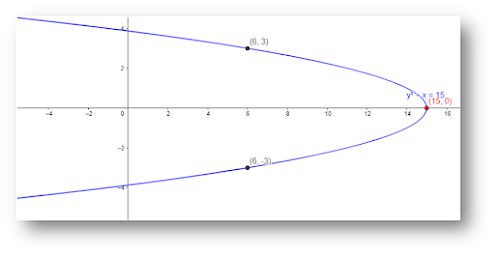
4. Parabola
Parabola adalah tempat kedudukan titik-titik pada bidang datar yang jaraknya ke satu titik dan garis tertentu sama. Titik tertentu disebut Titik Fokus dan garisnya direktris. Bentuk umum persamaan hiperbola:
Grafik fungsi parabola mempunyai 1 sumbu simetri dan 1 titik puncak.
Nilai 𝒑 dari persamaan parabola akan menetukan ciri-ciri tertentu dalam kurvanya:
- 𝒑>𝟎 maka parabola akan terbuka ke atas atau kesebelah kanan
- 𝒑<𝟎 maka parabola akan terbuka ke bawah atau kesebelah kiri
Hubungan antara nilai Diskriminan :
dengan titik potong grafik pada sumbu X atau Y
1. Jika D > 0 , maka grafik memotong sumbu X atau Y di dua titik yang berbeda.
2. Jika D = 0 , maka grafik menyinggung sumbu X atau Y di sebuah titik.
3. Jika D < 0 , maka grafik tidak memotong dan tidak menyinggung sumbu X
Contoh 8:
Jadikan bentuk persamaan parabola :
Contoh 9 : Tentukanlah perpotongan serta gambarkanlah kurva grafik kedua persamaan berikut:
VIDEO PEMBAHASAN MATERI DIATAS
DAFTAR REFERENSI
[1] Widayat, W.(2020). Matematika Ekonomi. Universitas Terbuka
[2] Sa'adah. U.N. dan Haryono, E. (2021). Matematika Ekonomi dan Bisnis. Pesona Press
[3] Dumairi. (2014). Matematika Terapan Untuk Ekonomi dan Bisnis. BPFE-Yogyakarta
[4] Kalangi, J.B. (2017). Matematika Ekonomi dan Bisnis (Edisi 3). Salemba Empat.









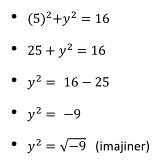




















0 Comments