A. PENGERTIAN KURVA NORMAL

Kurva Normal adalah histogram yang memiliki distribusi probabilitas yang kontinu. (Rini Yayuk Priyati, 2023 : 8.4).  Perhatikan Ilustrasi gambar berikut : 



Histogram memiliki distribusi yang patah-patah



Kurva Normal memiliki distribusi yang kontinu



Simpangan Baku 𝝈 adalah jarak antara mean dengan dua titik kiri dan kanan mean pada kurva  normal.


B.  KAIDAH – KAIDAH KURVA NORMAL

Kurva Normal memiliki beberapa kaidah-kaidah sebagai berikut: 


  1. Berdistribusi continue (tidak putus)
  2. Simetris (terhadap mean)
  3. Asimtotik (mendekati nol tapi tidak pernah nol)
  4. Besar kecilnya  𝝈 menentukan bentuk kurva


Contoh 1.
Bila diketahui rata-rata dari suatu distribusi normal adalah 8 dan simpangan bakunya adalah 2, maka gambarkanlah kurva normalnya!

Penyelesaian.
𝜇 = 8 dan  𝜎 = 2

Maka,
𝜇 + 𝜎 = 10
𝜇 + 2𝜎 = 12
𝜇 + 3𝜎 = 14

𝜇 − 𝜎 = 6
𝜇 − 2𝜎 = 4
𝜇 − 3𝜎 = 2


C.  KURVA NORMAL & PROBABILITAS 

Bila keseluruhan daerah kurva normal bernilai 1, maka luas daerah kurva normal  mengikuti kaidah sebagaimana gambar berikut: 



D.  NILAI Z

Kurva normal baku atau nilai z dipergunakan utnuk menunjukkan nilai variable random baku. Kurva normal baku menotasikan 𝜇 sebagai angka 0 dan 𝜎 sebagai 1. Rumus untuk menghitung z adalah:




Contoh 2.
Diketahui variable x memiliki distribusi normal dengan rata-rata 8 dan simpangan baku 2. Berapakah nilai z bila 𝑥1 = 12 dan 𝑥2 = 6?

Penyelesaian.
𝑧1 = (𝑥1−𝜇) / 𝜎
𝑧1 = (12−8) / 2 = 2
𝑧2 = (6−8)/2 = −1

Contoh 3.
Tentukan 𝑧 bila 𝑥=7,5 𝜇=15 dan 𝜎=4 ?

Penyelesaian.
𝑧 = (𝑥−𝜇)/𝜎
𝑧 = (7,5−15) / 4 = −1,875

E.  DAERAH KURVAL NORMAL BAKU

Untuk mengitung daerah kurva normal baku menggunakan kaidah pembahasan sebelumnya  sebagaimana gambar berikut:


Contoh 4.
Hitunglah luas daerah 𝑧=0 dan 𝑧=2 ? 

Penyelesaian.
luas daerah 𝑧 = 0 dan 𝑧 = 2 adalah 34,1% +13,6% = 47,7%

Contoh 5.
Hitunglah luas daerah 𝑧 = −2 dan 𝑧 = 2 ? 

Penyelesaian.
luas daerah 𝑧=0 dan 𝑧=2 adalah 34,1% +13,6 + 34,1% +13,6%  = 95,4%


F.  LUAS KURVA NORMAL ANTARA 0 DAN Z

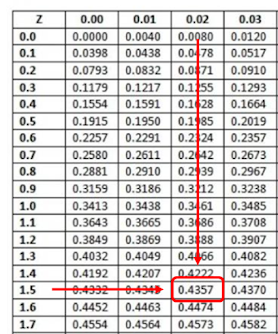
Untuk mengitung daerah kurva normal baku yang bukan merupakan angka bulat maka digunakanlah table distribusi normal baku.


Contoh 6.
Hitunglah luas daerah 𝑧=0 dan 𝑧=1,19 atau ditulis 𝑃( 0 ≤ 𝑍 ≤ 1,19 )  

Penyelesaian.
Dengan melihat tabel distribusi Z disamping
Maka didapatkan nilai 𝑃(0 ≤ 𝑍 ≤ 1,19) = 0,3830  

Contoh 7.
Hitunglah luas daerah 𝑃 (−1,81 ≤ 𝑍 ≤ 2,45 )  

Penyelesaian.
𝑃 (−1,81≤ 𝑍 ≤ 2,45) = 0,4649 + 0,4929 = 0,9578




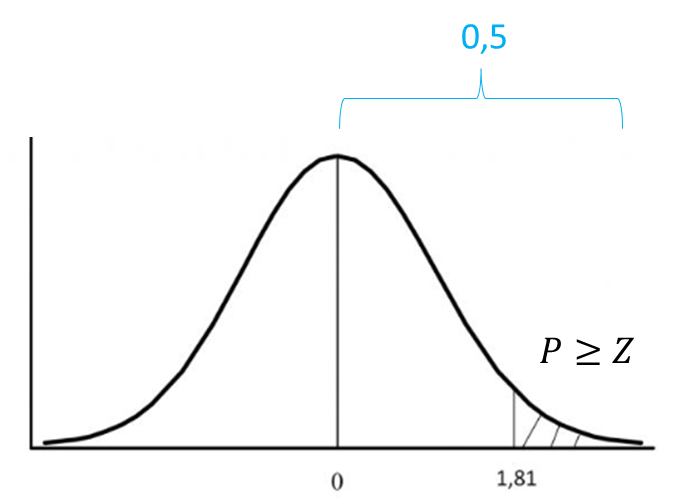
G.  LUAS KURVA NORMAL BAKU DI EKOR

Untuk menghitung daerah kurva normal baku yang berada di ekor atau paling ujung sebagaimana gambar dibawah, maka 𝑃≥𝑍 dapat dihitung dengan cara 0,5 dikurangi nilai antara 0 hingga 1,52.
1. Konsep 𝑃 ≥ 𝑍 

3. Menghitung nilai 0 ≥ 𝑃 ≥ 1,52

3. Menghitung 𝑃 ≥ 1,52
Perhitungannya adalah :  𝑃 ≥ 1,52 = 0,5000 − 0,4357 = 0,0643 

Contoh 8.
Tentukan luas area 𝑃(𝑍≥1,81)

Penyelesaian:
1. Konsep 𝑃 ≥ 𝑍 

2. Menghitung nilai 0 ≥ 𝑃 ≥ 1,81

3. Menghitung 𝑃 ≥ 1,52
Perhitungannya adalah : 𝑃 ≥ 1,52 = 0,5000 − 0,4649 = 0,0351 


H.  TEOREMA CENTRAL LIMIT

Teorema central limit atau dikenal rata-rata sampel (standard error) menggunakan rumus perhitungan sebagai berikut:
 

Keterangan:
𝑛 = jumlah sampel
𝜎/√𝑛 = simpangan baku

Contoh 9.
Berat rata-rata satu keranjang apel adalah 10 Kg dengan simpangan baku 2 Kg. Berapakah probabilitas bahwa 16 keranjang akan memiliki berat lebih dari 11,1 Kg?

Penyelesaian:
𝑧 = (𝑥−𝜇) / (𝜎/√𝑛) = (11,1−10) / (2/√16) = 2,2


(𝑍 ≥ 2,2) = 0,0139 , Sehingga probabilitas berat keranjang apel lebih dari sama dengan 11,1 adalah 13,9%


VIDEO PEMBELAJARAN


REFERENSI

  • Rini Yayuk Priyati, 2023. Statistika Ekonomi (Edisi 2), Tanggerang Selatan : Universitas  Terbuka.